
Return (checkDigit - Convert.ToInt32(imei. Public static bool VerifyLuhn(string imei)
/ Through Luhn algorithm to verify whether the number is legitimate, suitable for IMEI, bank cards, etc. Public static int CalcLuhnCheckDigit(string imei)ĪddValue += Convert.ToInt32(imei.ToString()) / Number that does not contain check bits Calculation what I did is like - But the check digit for the above IMEI is 4. I tried to find solution in google but I could not find correct answer using those algorithm. For example - 6C4BFFC0000004 Please help me with the algorithm. / Calculate the checkpoint by Luhn algorithm, which is suitable for IMEI, bank card, etc. I want to calculate check digit for a valid hexadecimal IMEI number.
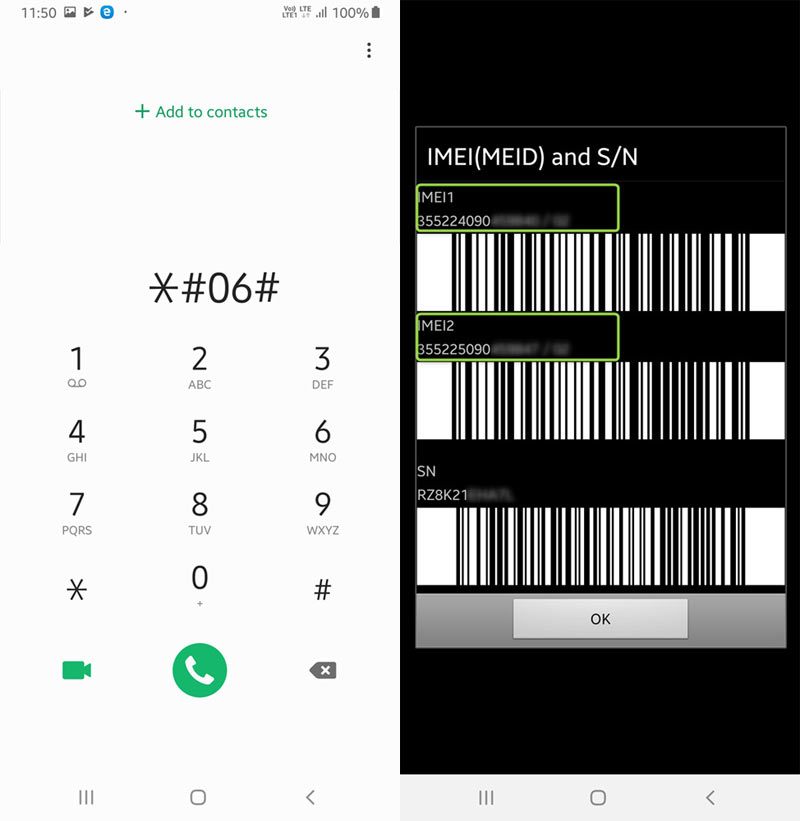
#Imei check digit algorithm verification#
Stay TS.06 IMEI Allocation and Approval ProcessIt stipulates that IMEI verification should pass Luhn algorithmThe calculation is as follows:ģ, C# code public class LuhnCalcCheckDigit IMEI codes are distributed uniformly by GSM (Global System for Mobile Communications, Global Mobile Communications Association), and BABT (British Approvals Board of Telecommunications) is authorized to stand trial. If 70-67=3,3 is the check bit.If the sum of all the numbers in the second step is equal to 0Ending, For example, 30, 40, 50, etc.Then the check is 0. Each SIM is internationally identified by its integrated circuit card identifier (ICCID). Step 3: The check bits can be obtained by subtracting the sum of the smallest integers ending at 0 and greater than the sum of the numbers obtained in step 2 from the sum obtained in step 2. IMEI Prefix, check imei, imei calculator, check digit, Luhn formula, imei last number, error IMEI, Luhn validator, Luhn check for IMEI, validate IMEI. The check digit is validated in three steps: Starting from the right, double a digit every two digits (e.g., 5 10).
#Imei check digit algorithm mod#
Step 2: Add each number from step 1 to the original number. check digit (d9) 7x (d1 + d4 + d7) + 3 (d2 + d5+ d8) + 9 (d3 + d6) mod 10. Step 1: Start with the first (lowest) position on the right and multiply by 2.
By checking ISO/IEC 7812-1:2017The file can see the explanation of the Luhn algorithm as follows:


 0 kommentar(er)
0 kommentar(er)
